ネタ | ポケットビリヤード道場 | スポーツ | まにあ道

今回は少し理屈について考えてみようと思います。第一弾は「ボールの動き」についてです。

では、まず下図を観て下さい。


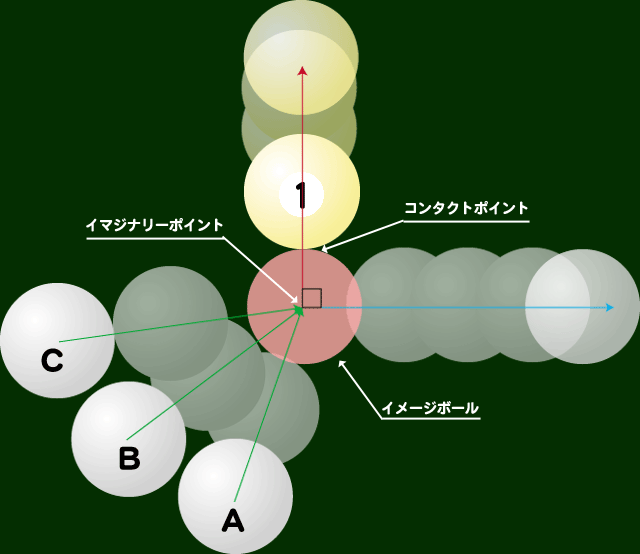
この図は１番を上方向（赤い矢印方向）に動かすにはどうしたら良いかを図解したものです。手玉はＡ〜Ｃまたはそれ以外の場所でも構いません。

手玉と先球は同じ大きさの球体ですから接する点は１点しかありません。すなわち図で１番を上に動かすにはどこから撞いてもコンタクトポイントのところで手玉と先球が接触すれば上に進むことになります。

仮に手玉と先球が当たる瞬間に手玉が無回転だったと仮定した場合１番に当たった後の手玉は１番の進行方向に対して直角に動きます。（図で言えば青いライン右方向）

手玉がＡのときには１番に当たった後に１番はたくさん転がりますが、手玉はあまり転がりません。逆に手玉がＣのときには１番に当たった後に１番はあまり転がりませんが、手玉はたくさん転がります。

ここでネタのストップショットの練習を思い出してください。「真っ直ぐに置いて無回転の状態で先球に当たると手玉は１番に当たった後にストップする。」と解説していますね。実はこれも上記の図を使って説明することが可能です。

真っ直ぐに置かれた配置でショットした場合、左右どちらにも直角となるので手玉は左右どちらにも動けません。そして、前述のように手玉の進む力はすべてが先球に伝わってしまうので推進力も失います。すなわち前に行くことも出来なくなります。これがストップショットの理屈です。

そして既に１／２の練習をされている方もいらっしゃるかもしれませんが、練習４を行うと手玉がサイドポケットにスクラッチすることがありませんか？それは、手玉と先球の関係がサイドポケットに向かってほぼ直角になっていることが原因です。ですから練習４を行う際には手玉が仮にスクラッチしても「正しく撞けている証拠」と捉えることが必要です。

逆にゲーム中には先球の直角方向にポケットがある場合にはスクラッチの危険があると解釈することも出来ます。スクラッチはほとんどのゲームでファールになりますので、それを上や下を撞くことで直角のラインから逸らして避けることが可能になるということですね。

図の中の薄い赤で示したボールはイメージボールといいます。そして、そのイメージボールの中心点をイマジナリーポイントと言います。

ビリヤードの教則本の多くは「イメージボールを想像し、イマジナリーポイントに向かって手玉の中心を撞けば先球はポケットされる」と書いてあります。教えるには非常に都合の良い理屈なんですが、私はこの理論を採用しません。なぜ採用しないのか？どうやって狙えば良いのか？というのは、また別の機会にネタにしますね。

今回は

「無回転で当たった手玉と先球は直角に分かれる」
「ストップショットの理屈」

この２点を理解して頂ければＯＫです。